
A New Ticket Price Algorithm
The 1.0.0 release of Decred will include the Decred Change Proposal, DCP-0001, the replacement of the existing stake difficulty, i.e. ticket price, algorithm as the first hard fork voting issue on mainnet. This is a major change and is being proposed to address the various issues that have come up with the stake difficulty (“sdiff” for short) since launch in February 2016. Decred launched with a sdiff algorithm that accomplished its basic design goal, which was to keep the ticket pool near its target size, but we have come to recognize several shortcomings and problems with the existing algorithm that were not apparent until it went into production use. The main problem is that a single interval where all the tickets are purchased leads to a persistent resonant mode, where very limited price exploration occurs, prices swing wildly and stakeholders compete on ticket fees. Replacing the existing sdiff algorithm with a new algorithm will lead to less wild variation in the ticket price and avoid the various problems associated with the existing algorithm. The properties of an ideal sdiff algorithm are related to:
- pool size stability
- price exploration
- simplicity
- relaxation time
- steady state behavior
which are explained in detail below. Currently, there are a few proposed sdiff algorithms from project developers and participants (raedah, animedow, and others) that we will be evaluating using a simulation harness developed by Dave Collins, dcrstakesim.
What is the purpose of the sdiff algorithm?
To understand an ideal sdiff algorithm, we must first understand the current sdiff algorithm. In order to keep PoS subsidy returns stable over time, Decred must maintain a stable ticket pool size, so we set the target size as 40,960 tickets. If the ticket pool size grows too large or too small, it can substantially alter the social contract between stakeholders and the network, disrupting the predictable nature of average time to vote a ticket, percentage of tickets that expire, and the rate of return. To maintain a target ticket pool size, the price of tickets must increase as the pool size goes up and decrease as the pool size goes down, to incentivize keeping the pool size near its target. Since users must observe the ticket price, choose to purchase and potentially wait to have their tickets mined, the ticket price must adjust on a interval basis. In what follows, further discussion of the sdiff interval size will be avoided and it is only mentioned here since it is a constraint imposed as a result of the ticket purchasing process.
The current sdiff algorithm
The current sdiff algorithm takes the historical values of pool size at the end of each interval and the number of tickets purchased in each interval for the last 20 sdiff intervals and the prior interval’s sdiff as inputs. The formula for the sdiff at interval N can be expressed as
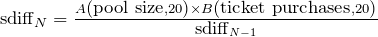
where A is a function of the pool size of the last 20 intervals, B is a function of ticket purchases of the last 20 intervals, and sdiff_N-1 is the previous interval’s sdiff. The function A scales roughly linearly with the pool size, so as the pool size grows, A does as well. The function B oscillates up and down based on ticket purchase history, where a full interval of ticket purchases sends B as high as 4, and an empty interval can send it as low as 0.25. Both functions A and B use an exponential moving average (“EMA”) over the last 20 intervals, meaning their values are “smoothed” relative to the past 10 days of ticket purchasing and pool size history.
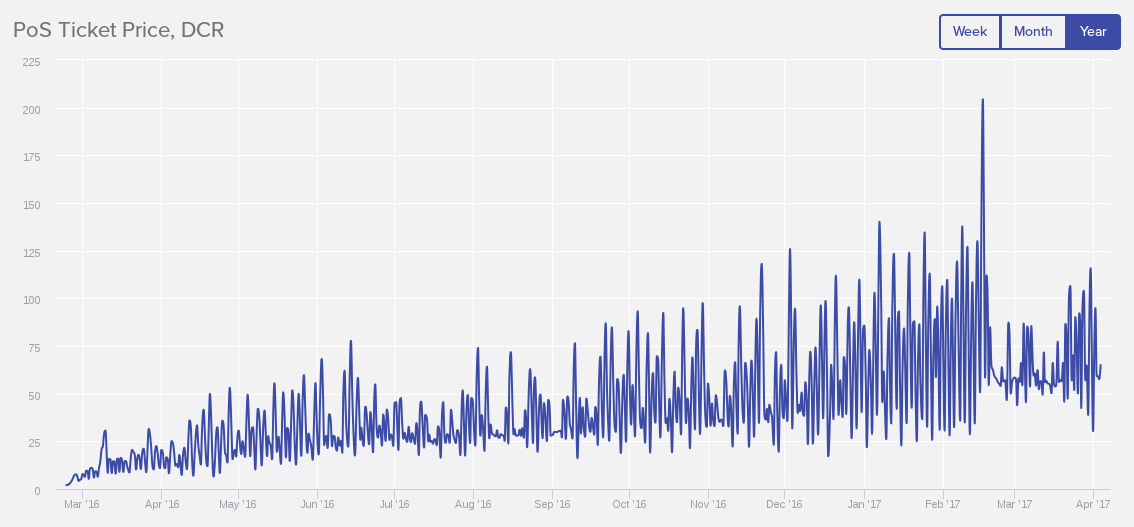
The current sdiff satisfies the dead minimum requirements of a sdiff algorithm: it maintains a relatively stable ticket pool size, the price goes up when the pool size grows, the price goes down when the pool size shrinks, and the price is intervaled. The ticket pool size has drifted as high as 45,034, but has more recently drifted downwards to the 41-42K range. When there is a full or nearly full interval of tickets, the ticket price jumps for 2 or 3 intervals, discouraging buying during those intervals, often to the point where these intervals are completely empty. Unfortunately, there are several problems that have emerged with the current sdiff algorithm after launch in February 2016.
Shortly after Decred’s launch we noticed that the ticket price had begun to oscillate with a period of either 3 or 4 intervals. 1 full ticket interval would lead to the price staying high for 2 or 3 intervals, where no tickets would be bought during those intervals, and then returning to a price that was close to that of the full ticket interval. This process has been going on for over a year at this point, and is an emergent resonant state that occurs due to the sdiff algorithm doing a poor job of price exploration. After 1 full interval occurs, the ticket price jumps up so much that it is outside the range of prices that people are willing to pay for tickets, and when the ticket price drops to a sustainable level, it is close to the previous full interval price. This resonant mode of the sdiff algorithm has led to fee wars during the low price intervals since the demand for tickets at a reasonable price is greater than the maximum supply of 2880 in the 1 full interval. Over time, the average price of a ticket has slowly increased, as seen in the graph of ticket price below.
If we look at the functional form of the sdiff algorithm, what is happening with the ticket price becomes much clearer. Recall that
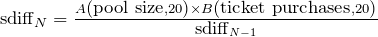
An ideal sdiff algorithm
Based on our experience with the current sdiff algorithm, we have come to realize there are several properties of an ideal sdiff algorithm that require consideration when finding a replacement algorithm:
- pool size stability
- price exploration
- simplicity
- relaxation time
- steady state behavior
These properties are explained in more detail below.
Pool size stability
The current algorithm does a decent job of keeping the pool size stable, but we’ve seen the pool size driven over 45K in certain conditions, which is less than ideal. Instead of only increasing the amplitude of price oscillations when the pool size was large, an ideal sdiff would steadily increase as the pool size grew, keeping the pool size closer to its target size.
Price exploration
Since 1 full interval causes the current sdiff to jump by up to a factor of 4, it does a very poor job of exploring the range of ticket prices users are willing to pay. If the maximum change in ticket price were bounded to a range where users are willing to buy them, it would be more reasonable to bound the changes to be a maximum increase of roughly 20% per interval, e.g. 1 full interval leads to a 20% increase in the ticket price next interval. An ideal sdiff would stay in the range of ticket prices that users are actually willing to pay since empty intervals only communicate there is zero demand, whereas a thinly bought interval gives quantitative feedback on demand. Similarly, in order to explore the ticket prices after a full interval, the sdiff should adjust downwards slowly, giving users the opportunity to buy at several prices above the price of the last full interval. This will allow for gradual increases in demand for tickets to lead to gradually increasing prices.
Simplicity
The current sdiff algorithm requires doing a bunch of calculations that involve pool size and ticket purchase history from the last 20 intervals, then dividing by the previous interval’s sdiff. The algorithm is complex and should be substantially simplified, so everyone can understand it more easily. Currently, the sdiff algorithm is
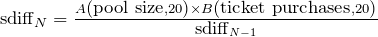
and I propose that an ideal sdiff algorithm would have the form
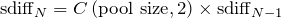
with some function C. This means only the pool size from the prior 2 intervals is needed to perform the calculation, and it scales the prior interval’s sdiff by a linear factor.
Relaxation time
When the current sdiff is driven by 1 full interval of tickets, it takes 2 or 3 empty intervals before it “relaxes” to its prior state, i.e. it takes 2 or 3 intervals for a perturbation to return to an equilibrium state. In order to prevent the possibility of driving the price with full intervals leading to a falling ticket pool size, we have the requirement that the relaxation time should be less than approximately 3 intervals. The particular scenario we’re trying to avoid here is 1 full interval (2880 tickets bought, 720 called for voting) followed by 3 or more empty intervals (0 tickets bought, 2160 or more called for voting). This places a constraint on the number of periods over which the ticket price must drop after a full interval.
Steady state behavior
Steady state ticket buying, i.e. 720 tickets per interval, with the current sdiff does not have the behavior one would hope for: maintaining a pool size over target should have an increasing price and a pool size under target should have a decreasing price. An ideal sdiff would have the property that when steady state ticket buying occurs, the price increases when the pool size is over target, and the price decreases when the pool size is under target. In terms of the proposed simplified form of the sdiff algorithm from above, this dictates that the function C should have 2 components, one a function of the delta between the last 2 pool sizes and the other a function of the delta between the last pool size and the target pool size.
Proposed replacement sdiff algorithms
A few alternative sdiff algorithms have recently been proposed by project developers and community members to date in a github issue for dcrd. The algorithms proposed so far include
-
track the percentage change in the pool size between the last 2 intervals and scale the ticket price according to that percentage, e.g. ticket pool goes up in size by at most 2160 on a full interval and down by at most 720 on an empty interval, so scale the ticket price by the change in ticket pool size divided by the ticket pool size, which bounds the interval-to-interval changes at 5.27% on the increase side and 1.75% on the decrease side (from raedah)
-
select a particular asymptotic function of the delta between the current pool size and the target pool size, which is approximately linear for small deltas and near exponential for larger deltas, and use the current average ticket price as a base when calculating a new ticket price (from animedow)
-
tally the total amount of coins currently locked for staking, then take a linear combination of the ratio of the locked coins to the target pool size and the ratio of the locked coins to the current pool size as the new ticket price (from coblee)
We will evaluate these algorithms and others that we receive from the community over the next 2 weeks, publish the results of the simulations and select what we consider to be the best choice. These simulations will be transparent, reproducible and all the assumptions will be laid out in detail at that time.
Evaluation via simulation
In order to select a new sdiff algorithm, Dave Collins has created a simulation harness, called dcrstakesim, which we will use to evaluate each algorithm. Dcrstakesim simulates each proposed sdiff algorithm on a fresh simulated mainnet chain, and it includes logic to mimic users buying tickets as a function of the yield at a given ticket price. Additionally, it caps the percentage of the coin supply being locked for tickets, to ensure it reflects to what we’ve seen to date. While the algorithms proposed thus far are a great start, we will be evaluating them according to the ideal sdiff criteria specified above, which likely means making additional modifications to what has already been proposed. If you’re keen to propose an algorithm, have a closer look at what’s already there or provide constructive criticism, join us on GitHub, the Decred Forum or our Slack chat.
